10. Applications of representation theory to physics problems

Representation theory can be used in many problems in physics to simplify calculations:

• molecular physics

• crystallography

• quantum mechanics

• particle physics

• …

• any system with a symmetry

10.1. Main example: vibrations of water molecules

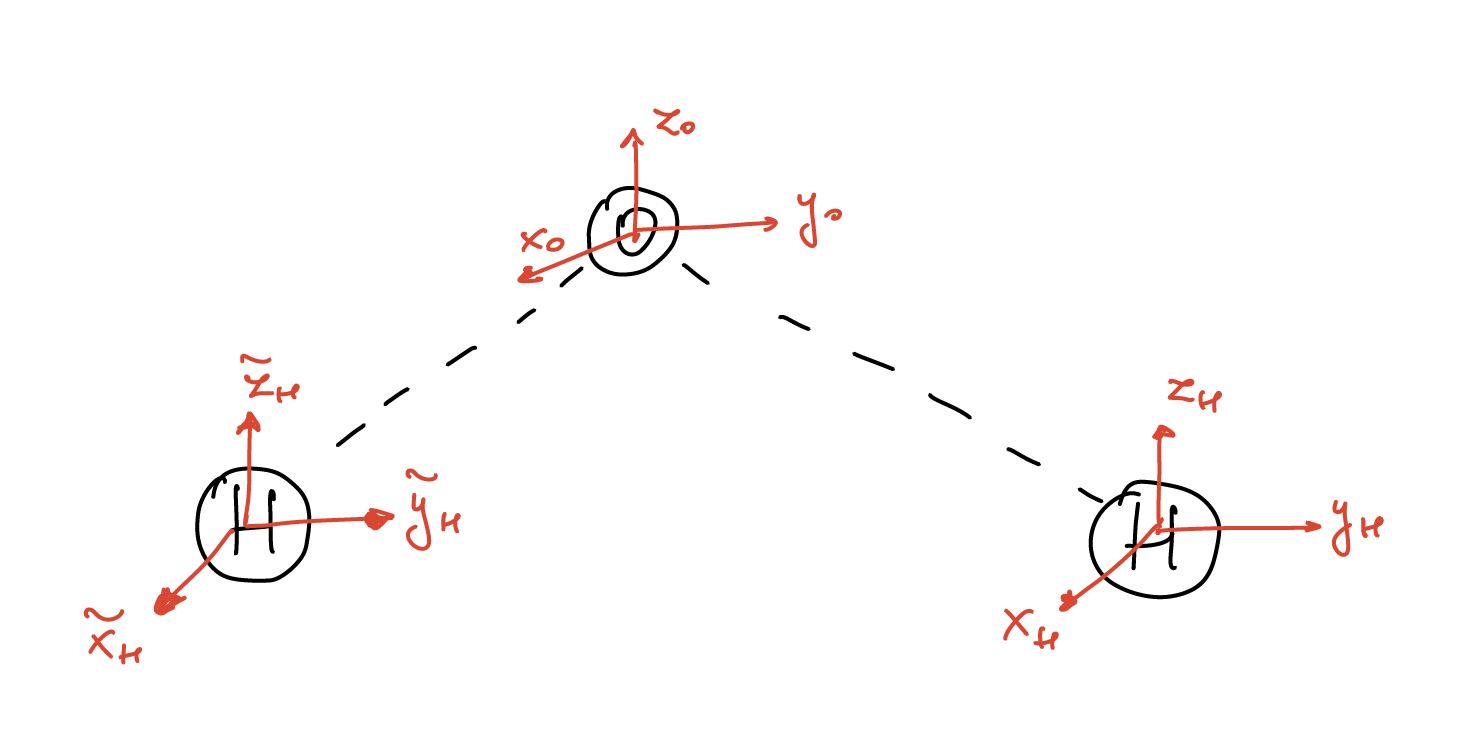
This molecule sits in the \(y-z\) plane with the \(x\)-axis pointing towards the reader.

There are four symmetries of this molecule:

• \(E\): identity

• \(C_2\): rotation by \(\pi\) in the \(x-y\) plane

• \(\sigma_{yz}\): reflection with respect to the \(y-z\) plane

• \(\sigma_{xz}\): reflection with respect to the \(x=z\) plane located at the oxygen atom

Multiplication table of this group is:

\[\begin{split} \begin{array}{c||c|c|c|c} &E&C_2&\sigma_{yz}&\sigma_{xz}\\ \hline \hline E&E&C_2&\sigma_{yz}&\sigma_{xz}\\ \hline C_2&C_2&E&\sigma_{xz}&\sigma_{yz}\\ \hline \sigma_{yz}&\sigma_{yz}&\sigma_{xz}&E&C_2\\ \hline \sigma_{xz}&\sigma_{xz}&\sigma_{yz}&C_2&E \end{array} \end{split}\]

This group of symmetries is called \(C_{2\nu}\) and it is isomorphic to the group \(\mathbb{Z}_2\times \mathbb{Z}_2\):

\[ \mathbb{Z}_2\times \mathbb{Z}_2=\{(0,0),(0,1),(1,0),(1,1)\} \]

with the binary operation given by addition of these two-dimensional vectors modulo 2.

In the following we will use the character table for \(C_{2\nu}\). The group \(C_{2\nu}\) is abelian with four elements, each of which gives one conjugacy class, implying that there are four irreducible representations, all of them one-dimensional:

\[\begin{split} \begin{array}{c||c|c|c|c} &E&C_2&\sigma_{yz}&\sigma_{xz}\\ \hline \hline A_1&1&1&1&1\\ \hline A_2&1&1&-1&-1\\ \hline B_1&1&-1&1&-1\\ \hline B_2&1&-1&-1&1 \end{array} \end{split}\]

Looking back at the water molecule, we can construct the representation generated by the nine vectors in the figure above: \((x_O,y_O,z_O,x_H,y_H,z_H,\tilde{x}_H,\tilde{y}_H,\tilde{z}_H)\). This provides the following nine dimensional representation \(\Gamma_9\):

\[\begin{split} M_E=\begin{pmatrix}1&0&0&0&0&0&0&0&0\\0&1&0&0&0&0&0&0&0\\0&0&1&0&0&0&0&0&0\\0&0&0&1&0&0&0&0&0\\0&0&0&0&1&0&0&0&0\\0&0&0&0&0&1&0&0&0\\0&0&0&0&0&0&1&0&0\\0&0&0&0&0&0&0&1&0\\0&0&0&0&0&0&0&0&1\end{pmatrix} \qquad M_{C_2}=\begin{pmatrix}-1&0&0&0&0&0&0&0&0\\0&-1&0&0&0&0&0&0&0\\0&0&1&0&0&0&0&0&0\\0&0&0&0&0&0&-1&0&0\\0&0&0&0&0&0&0&-1&0\\0&0&0&0&0&0&0&0&1\\0&0&0&-1&0&0&0&0&0\\0&0&0&0&-1&0&0&0&0\\0&0&0&0&0&1&0&0&0\end{pmatrix} \end{split}\]

\[\begin{split} M_{\sigma_{yz}}=\begin{pmatrix}1&0&0&0&0&0&0&0&0\\0&-1&0&0&0&0&0&0&0\\0&0&1&0&0&0&0&0&0\\0&0&0&1&0&0&0&0&0\\0&0&0&0&-1&0&0&0&0\\0&0&0&0&0&1&0&0&0\\0&0&0&0&0&0&1&0&0\\0&0&0&0&0&0&0&-1&0\\0&0&0&0&0&0&0&0&1\end{pmatrix} \qquad M_{\sigma_{yz}}=\begin{pmatrix}1&0&0&0&0&0&0&0&0\\0&-1&0&0&0&0&0&0&0\\0&0&1&0&0&0&0&0&0\\0&0&0&0&0&0&1&0&0\\0&0&0&0&0&0&0&-1&0\\0&0&0&0&0&0&0&0&1\\0&0&0&1&0&0&0&0&0\\0&0&0&0&-1&0&0&0&0\\0&0&0&0&0&1&0&0&0\end{pmatrix} \end{split}\]

We can calculate the characters of this representation

\[\begin{split} \begin{array}{c||c|c|c|c} &E&C_2&\sigma_{yz}&\sigma_{xz}\\ \hline \hline \Gamma_9&9&-1&1&3\\ \end{array} \end{split}\]

This representation is reducible and can be decomposed into irreducible representations:

\[ \langle \chi_{\Gamma_9},\chi_{A_1}\rangle=\frac{1}{4}(9\cdot 1+(-1)\cdot 1+1\cdot 1+3\cdot 1)=\frac{1}{4}(9-1+1+3)=3 \]

\[ \langle \chi_{\Gamma_9},\chi_{A_2}\rangle=\frac{1}{4}(9\cdot 1+(-1)\cdot 1+1\cdot (-1)+3\cdot (-1))=\frac{1}{4}(9-1-1-3)=1 \]

\[ \langle \chi_{\Gamma_9},\chi_{B_1}\rangle=\frac{1}{4}(9\cdot 1+(-1)\cdot(-1)+1\cdot 1+3\cdot (-1))=\frac{1}{4}(9+1+1-3)=2 \]

\[ \langle \chi_{\Gamma_9},\chi_{B_2}\rangle=\frac{1}{4}(9\cdot 1+(-1)\cdot (-1)+1\cdot (-1)+3\cdot 1)=\frac{1}{4}(9+1-1+3)=3 \]

Therefore

\[ \Gamma_9=3A_1\oplus A_2\oplus 2B_1\oplus 3B_2 \]

This decomposition can be understood in the following way:

• every particle has 3 translational degrees of freedom. Let us translate the molecule along the \(y\)-axis

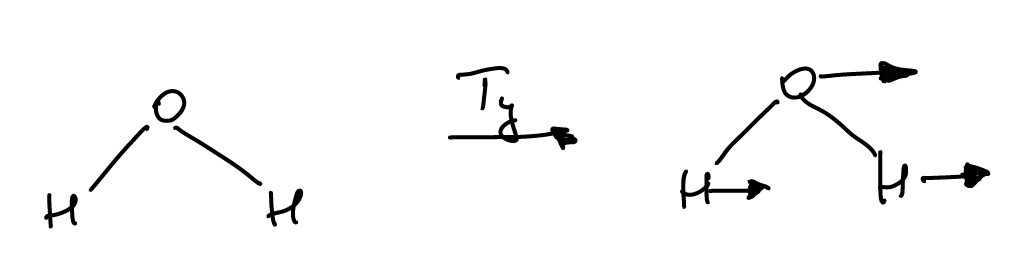
This defines a representation of \(C_{2\nu}\) since

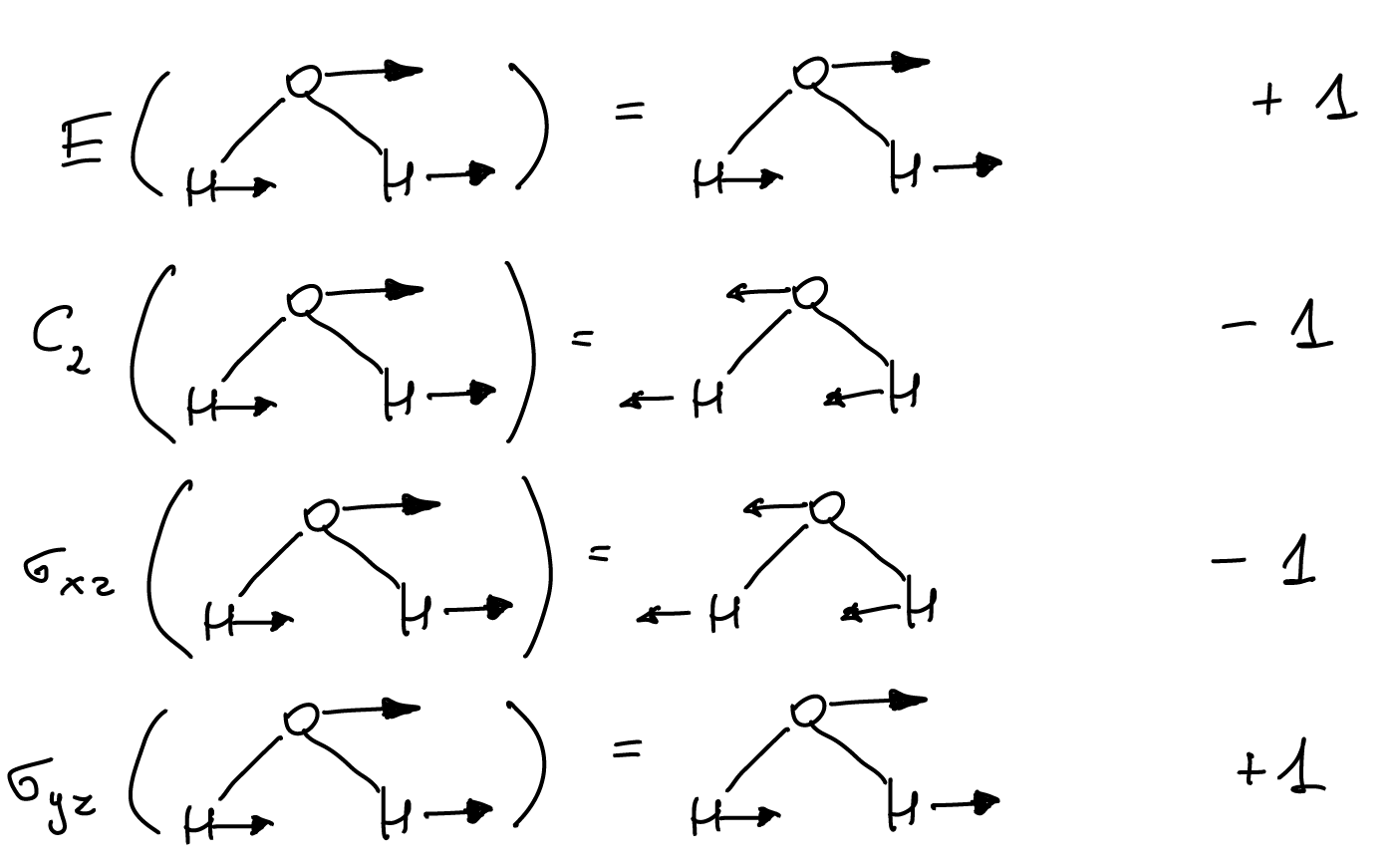
This is the same action as we found for the irreducible representation \(B_2\).

Similar for the translations \(T_x\) and \(T_z\). This can be summarized in the table below

\[\begin{split} \begin{array}{c||c|c|c|c|c} &E&C_2&\sigma_{yz}&\sigma_{xz}&irrep\\ \hline \hline T_x&1&-1&1&-1&B_1\\ \hline T_y&1&-1&-1&1&B_2\\ \hline T_z&1&1&1&1&A_1 \end{array} \end{split}\]

• every particle has three rotational degrees of freedom. Let \(R_z\) be the rotation in the plane perpendicular to the \(z\)-axis

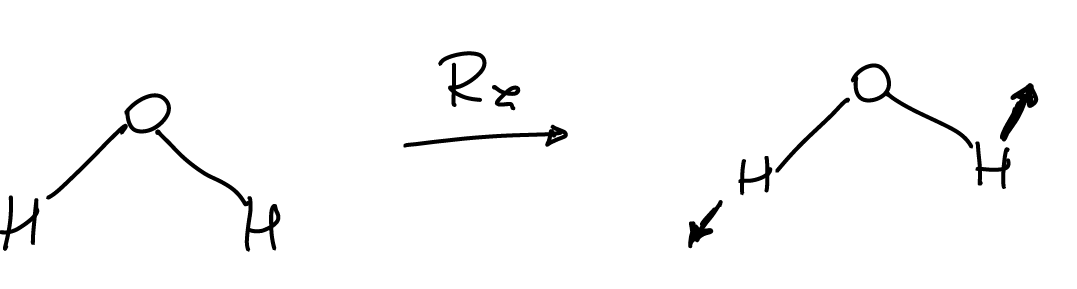
We can find the action of all symmetries on these vectors to find

\[\begin{split} \begin{array}{c||c|c|c|c|c} &E&C_2&\sigma_{yz}&\sigma_{xz}&irrep\\ \hline \hline R_x&1&-1&-1&1&B_2\\ \hline R_y&1&-1&1&-1&B_1\\ \hline R_z&1&1&-1&-1&A_2 \end{array} \end{split}\]

To summarize:

• translations: \(\Gamma_{\mathrm{trans}}=A_1\oplus B_1\oplus B_2\)

• rotations: \(\Gamma_{\mathrm{rot}}=A_2\oplus B_1\oplus B_2\)

Recall that \(\Gamma_9=3A_1\oplus A_2\oplus 2B_1\oplus 3B_2\). Then, after removing the translations and rotations we get:

\[ \Gamma_9-\Gamma_{\mathrm{trans}}-\Gamma_{\mathrm{rot}}=2A_1\oplus B_2=:\Gamma_{\mathrm{vib}} \]

we are left with three vibrational degrees of freedom. They correspond to:

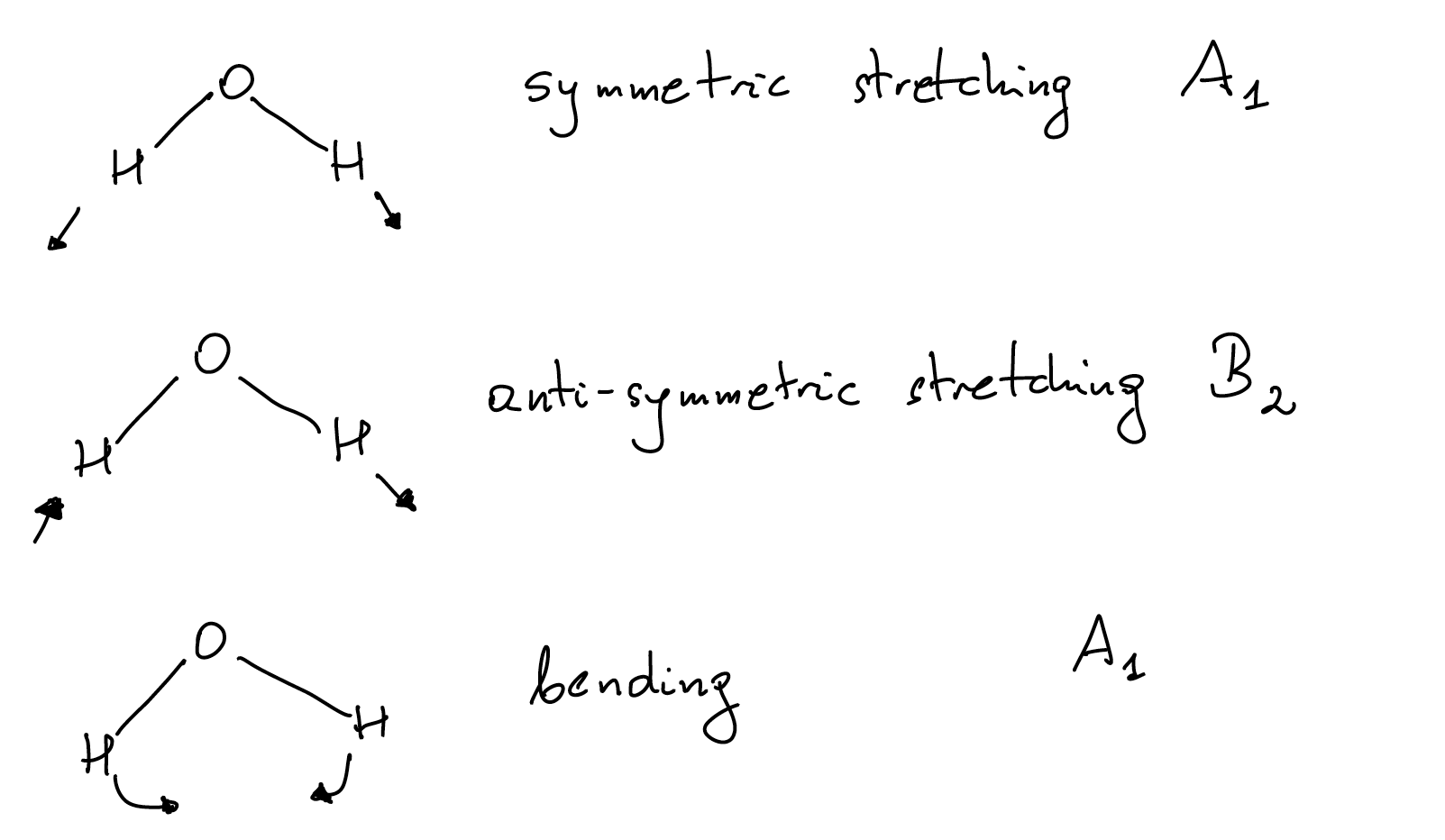
Each of these degrees of freedom will lead to a single normal mode with its own very well-defined frequency and energy that can be measured in experiments.